This automaton grows on a square grid in a fractal pattern
This is a rough draft I did while learning Python. It is unoptimized but pedagogical
You can make the size variable larger to expand the board, but this code gets slow for large boards
#!/usr/bin/python3.5
# assembles a grid (board) nxn in size
# first creates a list of n empty lists
# second, for each empty list (row) in board, append " " to each list n times
# this gives n independent objects (string characters) in each row rather than
# one object of length n in each row
def assemble_board(n):
board = [[] for i in range(n)]
for row in board:
for j in range(n):
row.append(" ")
return board
# takes an array/list/int and returns middle index as int
def find_midpoint(array):
if type(array) is list:
if len(array) % 2 != 0:
midpoint_index = len(array) // 2
return midpoint_index
else:
print("ERROR: EVEN ARRAY LENGTH")
elif type(array) is int:
if array % 2 != 0:
midpoint_index = array // 2
return midpoint_index
else:
print("ERROR: EVEN INTEGER")
else:
print("ERROR: NOT A LIST OR INTEGER")
# places an "X" at the middle point of the board
# determined by passing it an int, such as calling find_midpoint
def create_mid(y):
mid_index = find_midpoint(y)
board[mid_index][mid_index] = "X"
# takes in a list of cells or single cell and returns list of all neighboring cell
# can be run recursively
def find_neighbors(list_of_cells):
neighbors = []
if type(list_of_cells[0]) is int:
n1 = [list_of_cells[0] - 1, list_of_cells[-1]]
n2 = [list_of_cells[0], list_of_cells[-1] + 1]
n3 = [list_of_cells[0] + 1, list_of_cells[-1]]
n4 = [list_of_cells[0], list_of_cells[-1] - 1]
neighbors.append(n1)
neighbors.append(n2)
neighbors.append(n3)
neighbors.append(n4)
#print(neighbors)
return neighbors
else:
for each_cell in list_of_cells:
n1 = [each_cell[0] - 1, each_cell[-1]]
n2 = [each_cell[0], each_cell[-1] + 1]
n3 = [each_cell[0] + 1, each_cell[-1]]
n4 = [each_cell[0], each_cell[-1] - 1]
neighbors.append(n1)
neighbors.append(n2)
neighbors.append(n3)
neighbors.append(n4)
#print(neighbors)
return neighbors
# takes in list of cells - finds any cells with X's
def find_xs(stuff):
cells_on = []
for each_cell in stuff:
if board[each_cell[0]][each_cell[-1]] == "X":
cells_on.append(each_cell)
return cells_on
size = 23 # choose desired size of playing board
assembled_board = assemble_board(size) # assemble board passing size
board = assembled_board.copy() # create a list copy so not calling assemble_board
# *row prints each element of each list (rows), giving
# a nicer board print than default list diplay
midpoint_coord = [find_midpoint(size), find_midpoint(size)]
create_mid(size) # sets middle coord to 'X', represents turn 1
turn = 1
for row in board:
print(*row)
current_turn_cells_on = midpoint_coord
next_turn_cells_maybe_on = find_neighbors(current_turn_cells_on)
next_turn_cells_checkers = find_neighbors(next_turn_cells_maybe_on)
print("1 ", current_turn_cells_on, "2 ", next_turn_cells_maybe_on, "3 ", next_turn_cells_checkers)
for k in range(size // 2):
user_input = input("Next turn?")
if(user_input == "yes"):
for each_cell in next_turn_cells_maybe_on:
counter = 0
#print(each_cell[0],each_cell[-1])
next_turn_cells_checkers = find_neighbors(each_cell)
#print("next", next_turn_cells_checkers)
for cells in next_turn_cells_checkers:
#print("cells", cells)
if board[cells[0]][cells[-1]] == "X":
counter = counter + 1
#print("counter", counter)
if counter < 2:
board[each_cell[0]][each_cell[-1]] = "X"
for row in board:
print(*row)
#print("next_turn_cells_maybe_on", next_turn_cells_maybe_on)
#print("find_xs", find_xs(next_turn_cells_maybe_on))
current_turn_cells_on = find_xs(next_turn_cells_maybe_on)
#print("current", current_turn_cells_on)
next_turn_cells_maybe_on = find_neighbors(current_turn_cells_on)
print(find_neighbors(find_neighbors(midpoint_coord)))
print(midpoint_coord)
for row in board:
print(*row)
for row in board:
print(*row)
Sample outputs:
This is after 11 steps:
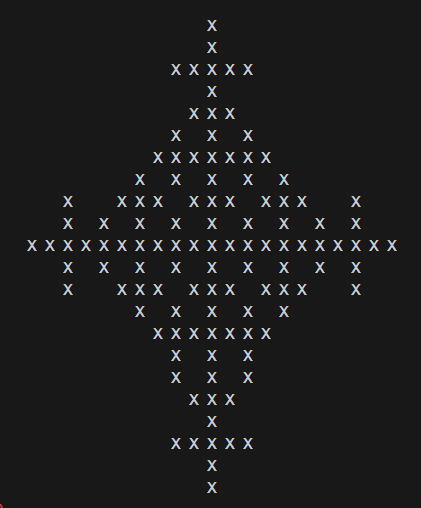
After many more:

You can try a more professional version along with others at OEIS. To try the Ulam-Warburton, select it from the Main Sequence dropdown.
You can read more about this automaton on Wikipedia and watch on Numberphile.